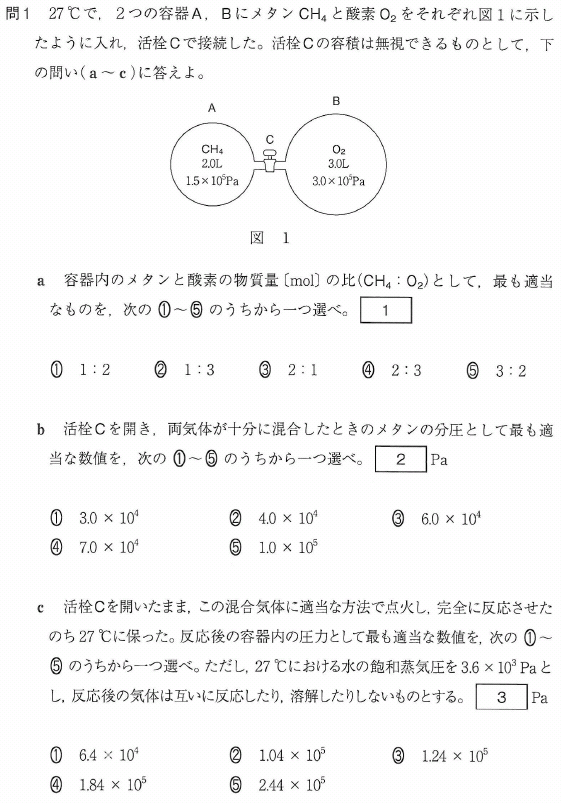
問１
a
　　状態方程式で各物質量を計算してもいいのですが、
　　CH_４とO_２を同一体積にした時の圧力で比較、又は
　　CH_４とO_２を同一圧力にした時の体積で比較、という手があります。計算早いです！
　　どちらも物質量の比が求められます。
　
　　では、CH_４とO_２を同一圧力３×１０^５Paにした時の体積で考えてみましょう。
　　CH_４は１L、O_２は３Lですね。
　　ということは、CH_４(mol)： O_２(mol)＝ １ ： ３ となります。いいでしょうか？
答［１］②

b
　　CH_４の体積は２Lから５Lになったので、圧力は２／５ 倍になります。
　　　１．５×１０^５Pa × （２／５） ＝ ６×１０^４Pa
答［２］③

c
　　CH_４燃焼の反応式を書き、分圧（Pa）を記入してみましょう。
　　　　　　　　CH_４＋　２O_２→　　CO_２＋　　２H_２O
　反応前　　 6×10^４18×10^４
　反応分　－6×10^４－12×10^４　 ＋6×10^４＋12×10^４
　反応後　　　　　　　    6×10^４　 　 6×10^４ 12×10^４

　　ここで、生じたH_２Oについて考えてみましょう。（重要ポイントです！）
　　12×10^４Paとなっていますね？　これは飽和水蒸気圧 3.6×10^３Pa を超えています。
　　このことから水蒸気は飽和状態で、この時の水蒸気圧は3.6×10^３Paだ ということです。
　　よって反応後の全圧は、
　　　6×10^４＋ 6×10^４＋ 0.36×10^４＝ 12.36×10^４≒ １．２４×１０^５Pa
答［３］③  

問１
a
　　Aの水素の体積が３Lから５Lになるだけです。
　　体積が５／３倍になるので、圧力は３／５倍になります。
　　ボイルの法則の式に入れずに、次のように計算するとちょとだけ早いですよ。
　　　２×１０^５×（３／５） ＝ １．２×１０^５Pa
答［１］②

b
　　２つのコックD、Eを開いた後、
　　水素の分圧P_H2は、
　　　P_H2＝２×１０^５×（３／６） ＝ １×１０^５Pa
　　一方、全圧は ２×１０^５Paですから、
　　気体Xの分圧P_Xは
　　　P_X ＋ P_H2 ＝ ２×１０^５Pa
　　　∴P_X ＝ １×１０^５Pa
　　　P_H2： P_X ＝ １：１　なので
　　H_２とXが １：１ で混合していることが分かります。
　　すなわち、H_２とXの分子量の単純平均が１７ということになります。
　　　∴ （２＋M_X）／２ ＝ １７
　　　∴ M_X ＝ ３２
　　分子量３２になるのは、選択肢の中ではO_２になります。
答［２］⑥

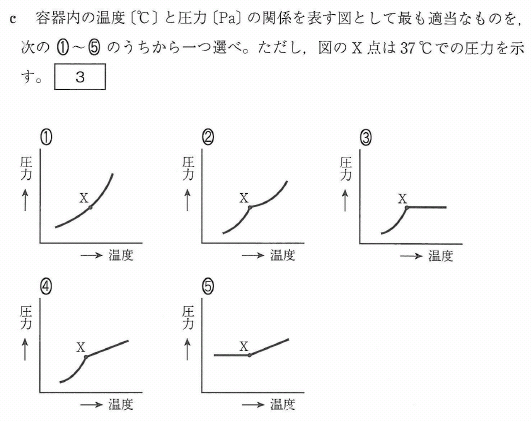
ｃ
　　温度を上げていった時、ある温度までは気体と液体が共存し、
　　この時の気体の圧力は飽和蒸気圧ですから、
　　上の温度対圧力のグラフでは蒸気圧曲線として表されることになりますね。
　　次に、液体がすべて蒸発して気体になってしまえば、通常の気体のふるまいですから
　　温度対圧力のグラフは傾きが一定の直線として表されます。
　　よって、蒸気圧曲線に正の傾きの直線が接続されたグラフが正解です。
答［３］④

問１
a
　　３７℃でちょうど液体がなくなった訳ですから、
　　化合物Aについて、
　　蒸気の圧力は飽和蒸気圧の２．５７×１０^４Pa、蒸気の体積は０．５L、蒸気の質量は０．７７ｇ です。
　　これを、状態方程式 PV ＝ wRT／M に代入すると、分子量Mが求められますね？
　　M ＝ wRT／PV
　　　 ＝０．７７×８．３×１０^３×３１０／２．５７×１０^４×０．５
　　　 ≒１５４．２
答［１］②

ｂ
　　２０℃で気体になっている化合物Aの質量wは、状態方程式を用いて
　　w ＝ MPV／RT
　　　 ＝ １５４ × １．２１ × １０^４ × ０．５／８．３ × １０^３ × ２９３
　　　 ≒ ０．３８ｇ
　　よって、液化した化合物Aは
　　０．７７－０．３８ ≒ ０．３９g
　　
　　∴液化した化合物Aの割合は、
　　（０．３９ × ０．７７） × １００ ≒ ５０．６%
答［２］②
　　２０℃のAの飽和蒸気圧が１．２１×１０^４Paなので、
　　仮にですが、３７℃→２０℃の液化分を圧力で示してあげると
　　２．５７×１０^４－１．２１×１０^４＝１．３６×１０^４Paです。
　　ですから、液化分の割合は
　　（１．３６×１０^４／２．５７×１０^４）×１００ でいいんじゃない！？
　　これで計算すると、約５３％となり答が違ってます・・・
　　このやり方スムーズでいいと思ったのに・・・
　　気づきましたか？
　　そうです。温度が変化しているんですね。
　　上の計算では、温度変化が圧力に反映されていないんですね。
　　ここからは一般的ではありませんが、
　　圧力の値を温度変化に対応した値に変えてやってみましょうか？
　　３７℃での２．５７×１０^４Paは、２０℃では２．５７×１０^４×（２９３／３１０）≒２．４３×１０^４Pa
　　この値を用いて３７℃→２０℃の液化分を圧力で示すと
　　２．４３×１０^４－１．２１×１０^４＝１．２２×１０^４Paです。
　　∴液化分の割合は
　　（１．２２×１０^４／２．４３×１０^４）×１００≒５０．２％ となりました！ 
　　（概数値で計算を続けているので、先ほどの答と少しずれていますが、
　　やり方は正しいです！）

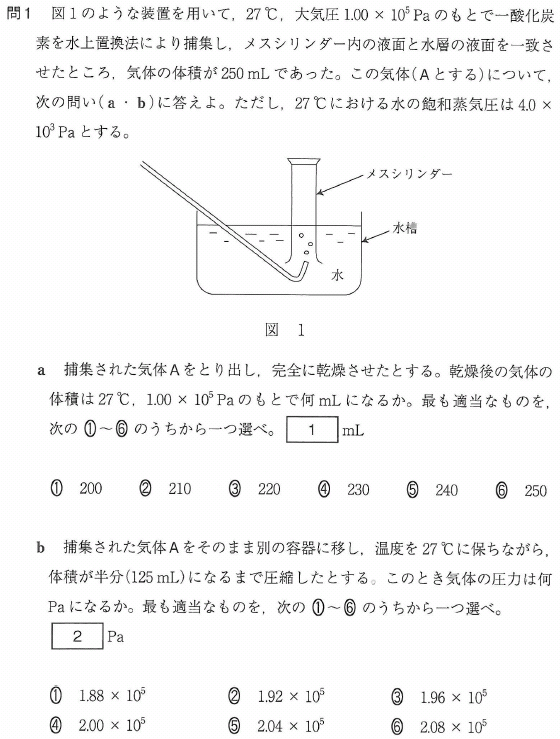
問１
a
　　水面を一致させているので、メスシリンダー内と外の気圧が同じになっています。
　　メスシリンダー内は水蒸気で飽和されていると考えて良いです。
　　メスシリンダー内のCOの分圧＋水蒸気の分圧＝大気圧　ですから
　　P_CO＝１×１０^５ － ４×１０^３＝１×１０^５ － ０．０４×１０^５＝０．９６×１０^５＝９．６×１０^４（Pa）
　　体積は２５０ｍLですね。
　　２７℃、１×１０^５Paのもとだと体積は何ｍL？
　　ボイルの法則の式に代入するのが普通ですが、次のやり方がちょっと早いです。
　　２５０ｍL×（９．６×１０^４／１×１０^５ ）＝２４０ｍL
　　「圧力と体積は反比例」を使いました。
答［１］⑤

ｂ
　　体積を１２５ｍLつまり １／２ 倍に圧縮するのですから、
　　COの圧力は２倍になります。
　　しかし、水蒸気は元々飽和状態だったので、圧縮しても飽和状態です。
　　この時の水蒸気の圧力は２７℃の飽和蒸気圧、つまり圧縮前と同じになります。
　　よって、圧縮後の全圧Pは
　　P＝９．６×１０^４×２ ＋ ４×１０^３
　　　＝１．９２×１０^５ ＋ ０．０４×１０^５
　　　＝１．９６×１０^５（Pa）
答［２］③
　　圧縮しても圧力が変わらないってどういうこと？　水蒸気はどこかへいっちゃったの？
　　って思いませんか？
　　水蒸気の一部が水滴に変化したのです。
　　（温度に応じた）決まった量しか水蒸気になれない訳ですから
　　圧縮すると、一部水滴になっていき、水蒸気圧が保たれる、という訳です。　　

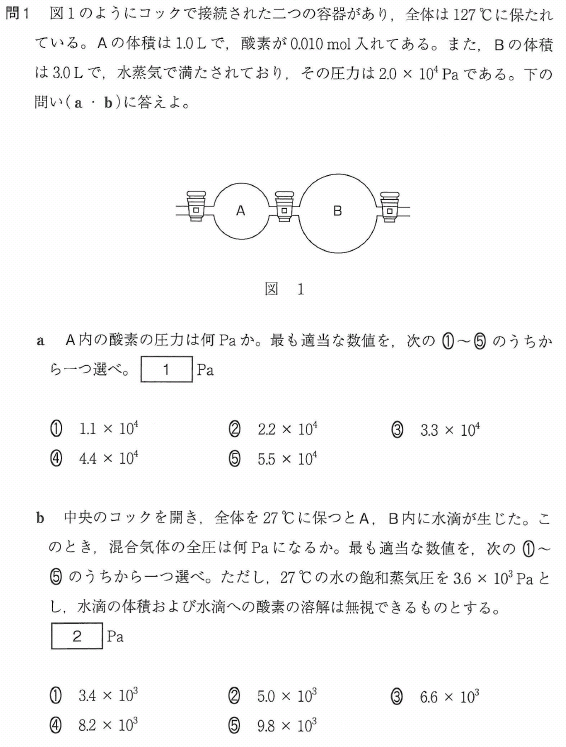
問１
a
　　コックはまだ開けられていません。容器Ａの中だけで考えます。状態方程式を使います。
　　　Ｐ＝ｎＲＴ／Ｖ
　　　　＝（０．０１×８．３×１０^３×４００／１．０）
　　　　≒３．３×１０^４（Ｐａ）
答［１］③

b
　　水滴が生じた状態なので、容器内は水蒸気で飽和している状態です。
　　ですから、この水蒸気の分圧は、飽和蒸気圧の３．６×１０^３Ｐａです。
　　一方、酸素の分圧は、
　　　Ｐ＝ｎＲＴ／Ｖ
　　　＝（０．０１×８．３×１０^３×３００／４．０）
　　　≒６．２×１０^３（Ｐａ）
　　∴容器内全圧は、
　　　３．６×１０^３ ＋ ６．２×１０^３（Ｐａ）＝９．８×１０^３（Ｐａ）
答［２］⑤

　　さて、この問題では、水蒸気の分圧をどう考えるかがポイントです。
　　水滴が生じていれば、容器内は水蒸気が飽和している状態ですから、
　　この時の水蒸気圧は、その温度での飽和水蒸気圧（温度に応じた決まった値）になります。
　　蒸発できる量には限度があり、それ以上は蒸発できない訳です。
　　その時の水蒸気の圧力が飽和蒸気圧ということですね。

　　仮に水滴が生じていなければ、水蒸気が飽和していない状況ですから、
　　この時の水蒸気の分圧Ｐは、ボイルシャルルの法則で求めればいいのです。
　
　
　　計算してみましょうか？
　　　２．０×１０^４×３．０／４００　＝　Ｐ×４．０／３００　ですね。
　　　Ｐ≒５．６×１０^３Ｐａとなりました。
　　この値は、飽和蒸気圧３．６×１０^３Ｐａを超えていますね。
　　飽和蒸気圧分を超えて蒸気にはなれないのですから
　　この時の水蒸気の圧力は３．６×１０^３Ｐａということになります。